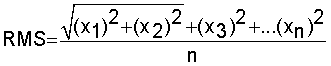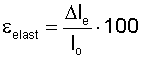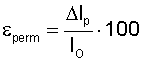EQUATIONS
The troughability of a conveyor belt can be estimated by using this equation,
where
m"G = belt mass in kg/m²
B = belt width in m
Sz = carcass thickness in mm
Cq = transverse rigidity factor (polyamide = 18, steel cord = 42)
TROUGHABILITY
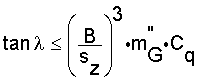
The modulus of elasticity is calculated by dividing the stress by the strain,
where
M = modulus of elasticity (ISO 9856)
F = force (N)
εelast = elastic elongation at the end of the specified number of cycles (N/mm)
In other words: The higher the modulus the lower the elastic elongation per unit stress. More
MODULUS OF ELASTICITY
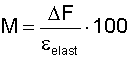
The modulus of elasticity can be used to calculate the tension force it exerts under a specific extension,
where
T = tension force
λ = modulus of elasticity
A = cross-sectional area
x = extension
l = length (m)
TENSION FORCE
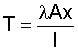
The minimum belt tensions for transmitting
the pulley peripheral forces are calculated as follows,
where
Fu = minimum peripheral force
C = coefficient C
f = artificial friction coefficient
L = conveyor length (m)
g = acceleration (m/s²)
qRo mass of revolving idler parts of top strand (kg/m),
qRu mass of revolving idler parts of bottom strand (kg/m),
qB mass of the belt on top strand (kg/m),
qG mass of the belt in bottom strand (kg/m),
H lift of the conveyor between discharge and loading area (m),
FS1 special main resistances,
FS2 special secondary resistances
MINIMUM PERIPHERAL FORCE
The required take-up length is calculated as follows,
where
SSp = take-up length (m)
L = conveyor length (m)
ε = belt elongation, elastic and permanent (%)
As a rough guideline, use 1,5 % elongation for textile belts
and 0,2 % for steel cord belts.
Note: For long-distance conveyors, dynamic start-up calculations
may be required, because not all elements are set in motion simultaneously,
due to the elastic properties of the conveyor belt.
TAKE-UP LENGTH
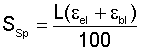
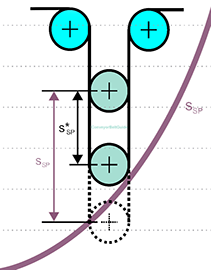
The coefficient C is a function of the length of the conveyor.
The total resistances without slope and special resistances are divided by the main resistances,
where
C = coefficient C
FH = primary resistances
FN = secondary resistances
COEFFICIENT C
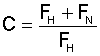
The Arrhenius equation describes the quantitative relation between reaction velocity and temperature
(the speed of chemical reactions increases with rising temperature),
where
k = temperature dependence of the rate constant (of a chemical reaction)
EA = activation energy
T = temperature (in Kelvin)
R = gas constant
Ae = prefactor (frequency factor)
ARRHENIUS EQUATION
where
σ = stress
v = period of strain oscillation
δ = phase lag between stress and strain
STRESS IN RUBBER
The storage modulus measures the stored energy, representing the elastic portion,
and the energy dissipated as heat, representing the viscous portion,
where
E' = storage modulus
σ = stress
ε = strain
δ = phase lag between stress and strain
STORAGE MODULUS
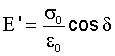
The loss modulus measures the stored energy, representing the elastic portion,
and the energy dissipated as heat, representing the viscous portion,
where
E'' = loss modulus
σ = stress
ε = strain
δ = phase lag between stress and strain
LOSS MODULUS
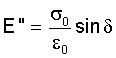
Internal friction is the force resisting motion between the elements making up a solid material
while it undergoes deformation. The tan δ is sometimes used to determine the indentation
loss of a conveyor belt cover (energy saving belts). E' and E'' should be as low as possible.
However, there are a number of misconceptions related to specifying E' and E''.
Where
tan δ = internal friction of a rubber
E' = storage modulus (N/mm²)
E'' = loss modulus (N/mm²)
INTERNAL FRICTION
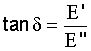
Where
v = belt velocity (m/s),
lvth = theoretical volume flow (m³/h),
ρ = bulk density of the conveyed material (t/m³),
φSt = coefficient for determination of the volume flow.
LENGTH RELATED MASS FLOW (m³/h)
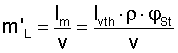
Where,
PB0 = braking factor related to the rated torque of all drive motors,
ηges = overall efficiency of all transmission elements between motor and pulley shaft,
PMerf = total capacity of the drive motors required in a steady operating state,
PMinst is the total installed capacity of the drive motors (N).
BRAKING FACTOR
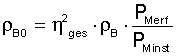
Where
g = gravity (9,81 m/s²)
m'Li = mass of the conveyed material, uniformly distributed across a section of the conveyor (kg/m)
m'G = length related mass of the conveyor belt (kg/m)
IRo = idler spacing in top run (m)
hrel = maximum belt sag related to the spacing between the carry idlers (%)
MINIMUM BELT TENSION FOR BELT SAG LIMITATION (top side, loaded)
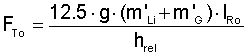
Where
g = gravity (9,81 m/s²)
m'G = length related mass of the conveyor belt (kg/m)
IRu = idler spacing in bottom run (m)
hrel = maximum belt sag related to the spacing between the carry idlers (%)
MINIMUM BELT TENSION FOR BELT SAG LIMITATION (bottom side, unloaded)
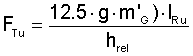
Where
f = friction factor in top and bottom run
L = conveyor length (m)
g = gravity acceleration (m/s²)
m'R = mass of the idlers (kg/m)
m'G = length related mass of the conveyor belt in both runs (kg/m)
m'L = mass of the conveyor belt with an evenly distributed load (kg/m)
δ = even inclination of the conveyor (°)
PRIMARY RESISTANCES IN AN EVENLY TILTED CONVEYOR
The Voigt model consists of a Newtonian damper and Hookean elastic spring connected in parallel.
It is used to explain the creep resp. relaxation behaviour of polymers.
Where
η = dynamic viscosity
τ = total stress
γ = total deformation
D = shear rate
G = shear modulus
VOIGT MODEL
Where
C = coefficient (main resistance factor)
f = resistance coefficient
L = belt length (m)
g = acceleration (m/s²)
qRO = mass of the idlers on top side (kg/m)
qRU = mass of the idlers on bottom side (kg/m)
qB = belt mass (kg/m)
qG = mass of the conveyed material (kg/m)
H = lift (m)
FS1 = special main resistances
FS2 = special secondary resistances
PERIPHERAL FORCE
Where
qG = conveying mass (kg/m)
H = lift (m)
g = acceleration (m/s²)
SLOPE RESISTANCE
Where
m'G = length related mass of the conveyor belt (kg/m)
g = acceleration (m/s²)
b = width (mm)
δ = troughing angle
l = idler length (mm)
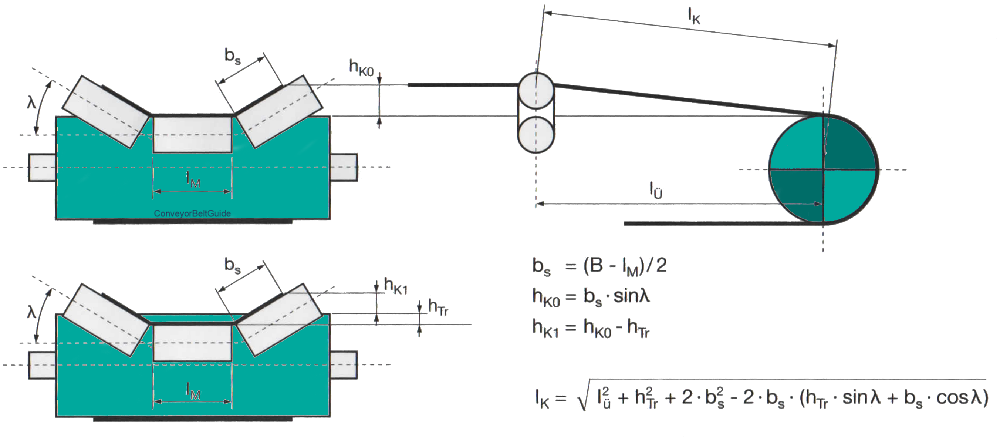
B = belt width (mm)
Tx = drive traction
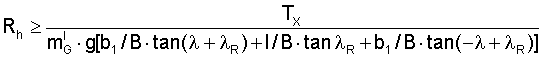
The E-Modulus (Young's modulus) defines the relationship between stress (force per unit area)
and strain (proportional deformation) in a belt,
where
ΔL = amount by which the length changes (mm)
F = force
Ao = original cross-sectional area
Lo = original length (mm)
ELASTIC MODULUS
Where
F = resistances to motion
v = belt speed
DRIVE POWER
Where
FH = primary resistances (idlers, belt indentation, etc.)
FN = secondary resistances (feeding, scrapers etc.)
FS = extraordinary resistances
FSt = gradient resistances
RESISTANCES TO MOTION
Where
FGH is the downhill force
FG is the weight force
Gravity acts straight down (= the weight of the conveyor belt) and the support force acts away from the conveyor. Since the conveyor is sloped, there is a net force acting down the slope.
DOWNHILL FORCE
The belt friction equation relates the hold-force to the load-force when a belt is is wound around a pulley,
where
e = 2,7183
EYTELWEIN'S EQUATION
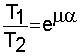
The RMS is the square root of the arithmetic mean of the squares of the values.
Please also see here.
ROOT MEAN SQUARE